Dihedral Rigidity and Deformation

Abstract

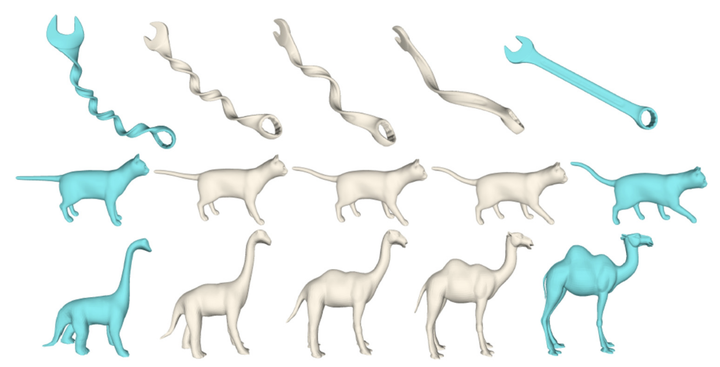
We consider defining the embedding of a triangle mesh into $\mathbb{R}^3$, up to translation, rotation, and scale, by its vector of dihedral angles. Theoretically, we show that locally, almost everywhere, the map from realizable vectors of dihedrals to mesh embeddings is one-to-one. We experiment with a heuristic method for mapping straight-line interpolations in dihedral space to interpolations between mesh embeddings and produce smooth and intuitively appealing morphs between three-dimensional shapes.

Carlos Rojas

Assistant Professor

My research interests include bioinformatics, computing education, visualization, and machine learning.